Contoh Soal Usaha pada Bidang Miring dan Pembahasan Lengkap
- Konsep Dasar Usaha dan Komponen Gaya di Bidang Miring
- Contoh Soal Usaha pada Bidang Miring Tanpa Gesekan
- Contoh Soal Usaha dengan Pengaruh Gaya Gesek
- Analisis Usaha Menggunakan Perubahan Energi Kinetik
- Tips Menghindari Kesalahan Umum dalam Perhitungan
- Mengoptimalkan Pemahaman Konsep Mekanika Lanjutan
Memahami konsep mekanika klasik sering kali menjadi tantangan tersendiri bagi para siswa, terutama saat berhadapan dengan contoh soal usaha pada bidang miring. Dalam studi fisika, usaha didefinisikan sebagai hasil kali antara gaya yang menyebabkan perpindahan dengan besarnya perpindahan itu sendiri. Namun, pada lintasan yang miring, perhitungan menjadi sedikit lebih kompleks karena adanya keterlibatan sudut elevasi yang memengaruhi komponen gaya yang bekerja pada benda.
Ketika sebuah benda diletakkan di atas bidang miring, gaya gravitasi tidak lagi bekerja sepenuhnya searah dengan arah gerak benda. Gaya berat tersebut akan terurai menjadi dua komponen utama, yaitu komponen yang sejajar dengan bidang miring dan komponen yang tegak lurus terhadap bidang miring. Penguasaan terhadap penguraian vektor ini adalah kunci utama agar Anda dapat menyelesaikan setiap persoalan fisika terkait usaha dan energi dengan akurasi tinggi.
Konsep Dasar Usaha dan Komponen Gaya di Bidang Miring
Sebelum masuk ke dalam berbagai variasi contoh soal, sangat penting bagi kita untuk menyamakan persepsi mengenai variabel-variabel yang terlibat. Secara umum, rumus usaha dinyatakan dengan $W = F \cdot s$, di mana $W$ adalah usaha (Joule), $F$ adalah gaya (Newton), dan $s$ adalah perpindahan (meter). Pada bidang miring, gaya $F$ yang digunakan dalam rumus haruslah gaya yang total atau resultan gaya yang searah dengan lintasan perpindahan.
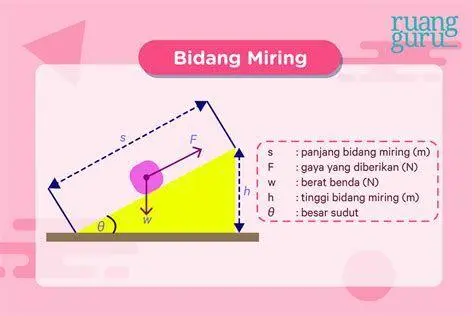
Mari kita tinjau sebuah balok bermassa $m$ yang berada pada bidang miring dengan sudut kemiringan $\theta$. Komponen gaya berat yang searah dengan kemiringan bidang (menuju bawah) adalah $mg \sin \theta$. Sementara itu, komponen gaya berat yang menekan bidang secara tegak lurus adalah $mg \cos \theta$. Jika benda bergerak tanpa gesekan (licin), maka gaya penggerak utamanya hanyalah komponen gravitasi tersebut. Namun, dalam kondisi nyata, kita sering menjumpai adanya gaya gesek yang arahnya selalu berlawanan dengan arah gerak benda.

Parameter Penting dalam Perhitungan
Berikut adalah tabel ringkasan komponen gaya yang sering muncul dalam soal-soal fisika mekanika untuk memudahkan Anda melakukan identifikasi variabel:
| Simbol | Nama Komponen | Rumus/Keterangan |
|---|---|---|
| $W_{grav}$ | Gaya Berat | $m \cdot g$ |
| $F_x$ | Komponen Sejajar Bidang | $mg \sin \theta$ |
| $F_y$ | Komponen Tegak Lurus Bidang | $mg \cos \theta$ |
| $f_k$ | Gaya Gesek Kinetis | $\mu_k \cdot N$ (di mana $N = mg \cos \theta$) |
| $W$ | Usaha Total | $\Sigma F \cdot s$ |
Contoh Soal Usaha pada Bidang Miring Tanpa Gesekan
Mari kita mulai dengan skenario paling sederhana untuk membangun logika dasar. Perhatikan soal berikut: Sebuah balok dengan massa 10 kg dilepaskan dari puncak bidang miring yang licin dengan sudut kemiringan 30 derajat. Jika panjang lintasan bidang miring adalah 5 meter, berapakah usaha yang dilakukan oleh gaya gravitasi hingga balok sampai di dasar?
Pembahasan:
- Diketahui: $m = 10\text{ kg}$, $\theta = 30^\circ$, $s = 5\text{ m}$, $g = 10\text{ m/s}^2$.
- Ditanya: Usaha ($W$).
- Langkah 1: Cari komponen gaya gravitasi yang searah bidang miring. $F = mg \sin 30^\circ = 10 \cdot 10 \cdot 0,5 = 50\text{ N}$.
- Langkah 2: Gunakan rumus usaha. $W = F \cdot s = 50\text{ N} \cdot 5\text{ m} = 250\text{ Joule}$.
Dalam kasus ini, karena bidang licin, tidak ada gaya penghambat. Usaha yang dilakukan oleh gaya gravitasi sepenuhnya berubah menjadi energi kinetik balok di dasar bidang miring. Perlu dicatat bahwa gaya normal tidak melakukan usaha karena arahnya tegak lurus ($90^\circ$) terhadap arah perpindahan, sehingga nilai $\cos 90^\circ = 0$.
Contoh Soal Usaha dengan Pengaruh Gaya Gesek
Kondisi yang lebih menantang adalah ketika permukaan bidang miring memiliki tingkat kekasaran tertentu. Misalkan sebuah benda bermassa 5 kg ditarik ke atas sepanjang bidang miring (sudut $37^\circ$, $\sin 37^\circ = 0,6$) dengan gaya luar sebesar 100 N. Jika koefisien gesek kinetis antara benda dan bidang adalah 0,2 dan benda berpindah sejauh 10 meter, hitunglah usaha total yang dilakukan pada benda.
Pembahasan Sistematis:
- Identifikasi Gaya Penarik: $F_{pull} = 100\text{ N}$.
- Identifikasi Gaya Penghambat 1 (Gravitasi): $F_g = mg \sin 37^\circ = 5 \cdot 10 \cdot 0,6 = 30\text{ N}$.
- Identifikasi Gaya Penghambat 2 (Gesek): Pertama cari gaya normal $N = mg \cos 37^\circ = 5 \cdot 10 \cdot 0,8 = 40\text{ N}$. Maka, $f_k = \mu_k \cdot N = 0,2 \cdot 40 = 8\text{ N}$.
- Hitung Resultan Gaya: $\Sigma F = F_{pull} - (F_g + f_k) = 100 - (30 + 8) = 62\text{ N}$.
- Hitung Usaha Total: $W_{total} = \Sigma F \cdot s = 62 \cdot 10 = 620\text{ Joule}$.
"Usaha total adalah jumlah skalar dari setiap usaha yang dilakukan oleh masing-masing gaya yang bekerja pada sistem tersebut." - Prinsip Kerja dan Energi.
Analisis Usaha Menggunakan Perubahan Energi Kinetik
Selain menggunakan pendekatan gaya, kita juga bisa menyelesaikan contoh soal usaha pada bidang miring dengan menggunakan Teorema Usaha-Energi. Teorema ini menyatakan bahwa usaha total yang dilakukan pada suatu benda sama dengan perubahan energi kinetiknya ($W = \Delta EK$). Pendekatan ini sangat berguna jika dalam soal diketahui kecepatan awal dan kecepatan akhir benda namun gaya-gayanya sulit diuraikan.
Misalnya, jika sebuah mobil mainan meluncur ke bawah dan kecepatannya berubah dari 2 m/s menjadi 6 m/s pada lintasan miring sepanjang 4 meter, kita bisa langsung menghitung usaha total tanpa harus tahu sudut kemiringannya, asalkan massa mobil diketahui. Ini membuktikan bahwa parameter fisika saling berkaitan erat dalam satu kesatuan hukum alam.

Tips Menghindari Kesalahan Umum dalam Perhitungan
Banyak siswa sering terjebak pada penggunaan fungsi trigonometri antara $\sin$ dan $\cos$. Sebagai aturan praktis yang mudah diingat, gunakan sinus untuk komponen gaya yang menyebabkan benda meluncur (sejajar bidang) dan kosinus untuk komponen gaya yang menekan bidang (menentukan gaya normal). Selain itu, pastikan satuan massa selalu dalam kilogram (kg) dan perpindahan dalam meter (m) agar hasil usaha tetap dalam satuan standar internasional yaitu Joule.
Seringkali, kesalahan kecil seperti lupa memasukkan gaya gesek atau salah menentukan arah gaya dapat mengakibatkan jawaban yang sangat jauh berbeda. Oleh karena itu, menggambar diagram bebas (Free Body Diagram) sebelum melakukan perhitungan numerik sangat disarankan untuk menjaga logika berpikir tetap terstruktur.
Mengoptimalkan Pemahaman Konsep Mekanika Lanjutan
Setelah mempelajari berbagai variasi contoh soal usaha pada bidang miring, Anda seharusnya kini memiliki kepercayaan diri lebih dalam menghadapi persoalan dinamika gerak. Fisika bukan sekadar menghafal rumus, melainkan memahami bagaimana setiap gaya berinteraksi satu sama lain dalam ruang dan waktu. Usaha pada bidang miring hanyalah satu pintu masuk menuju konsep yang lebih besar seperti hukum kekekalan energi mekanik dan daya.
Langkah selanjutnya yang sangat direkomendasikan adalah mencoba mengerjakan soal-soal dengan kombinasi gaya luar yang membentuk sudut tertentu terhadap bidang miring atau sistem katrol yang dihubungkan dengan bidang miring. Dengan memperbanyak latihan pada kasus-kasus kompleks, intuisi fisika Anda akan semakin tajam, memungkinkan Anda untuk melihat pola-pola matematis di balik fenomena fisik yang terjadi di sekitar kita sehari-hari. Teruslah bereksperimen dengan angka dan logika, karena penguasaan mekanika adalah fondasi dari seluruh ilmu teknik dan teknologi modern.


What's Your Reaction?
-
0
 Like
Like -
0
 Dislike
Dislike -
0
 Funny
Funny -
0
 Angry
Angry -
0
 Sad
Sad -
0
 Wow
Wow




